Dwa tartaki

Limit pamięci: 32 MB

Wdłuż głównej rzeki Bajtocji, która oczywiście płynie ze szczytu góry w dół, rośnie drzew. Drzewa owe zasłaniały widok królowi, więc wbrew protestom ekologów postanowił je ściąć. Żeby drewno się nie zmarnowało, każde drzewo po ścięciu trzeba dostarczyć do tartaku.

Drzewa mogą być spławiane tylko w dół rzeki. Przy ujściu znajduje się już jeden działający tartak, ale król postanowił przy okazji zbudować dwa kolejne.

Tobie przypadła ważna rola wybrania miejsca budowy nowych tartaków, tak aby koszt transportu drewna był jak najmniejszy.

Transport jednej tony drewna na odległość kilometra kosztuje jeden grosz.

Zadanie

Napisz program, który:

• wczyta ze standardowego wejścia liczbę drzew, ich wagi i położenie,
• obliczy minimalny koszt transportu drewna do tartaków,
• wypisze wynik na standardowe wyjście.

Wejście

W pierwszym wierszu wejścia znajduje się jedna liczba całkowita - liczba drzew (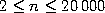). Drzewa są ponumerowane od do , w porządku od źródła rzeki do ujścia. Każdy z kolejnych wierszy zawiera dwie dodatnie liczby całkowite oddzielone pojedynczym odstępem. Wiersz 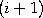-szy zawiera: 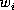- masę (w tonach) 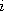-tego drzewa i 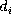- odległość (w kilometrach) pomiędzy drzewam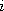i i 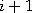(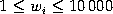, 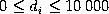). Ostatnia z tych liczb, 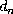, jest odległością od drzewa numer do ujścia rzeki. Wiadomo, że koszt transportu całego drewna do tartaku przy ujściu nie przekroczy 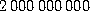groszy.

Wyjście

Pierwszy i jedyny wiersz wyjścia powinien zawierać jedną liczbę całkowitą: minimalny koszt transportu drewna do tartaków.

Przykład

Dla danych wejściowych:

9
1 2
2 1
3 3
1 1
3 2
1 6
2 1
1 2
1 1

poprawną odpowiedzią jest:

26

Obrazek pokazuje optymalne rozmieszczenie tartaków dla przykładowego testu. Drzewa zostały zaznaczone kółkami, wagi drzew są podane pod kółkami. Tartaki zostały zaznaczone na czarno. Dla tego rozmieszczenia, koszt transportu drewna jest równy: .

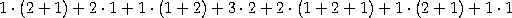Autor zadania: Wojciech Rytter.